Output a scalar:
Linear regression:
y = W x + b = ∑ i = 1 n w i x i + b y=Wx+b=\sum\limits_{i=1}^n{w_ix_i}+b y = W x + b = i = 1 ∑ n w i x i + b L = ∑ i = 1 n ( y i − y ^ i ) 2 L=\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2 L = i = 1 ∑ n ( y i − y ^ i ) 2
Polynomial regression:
y = ∑ i = 1 n w i x i + b y=\sum\limits_{i=1}^n{w_ix^i}+b y = i = 1 ∑ n w i x i + b
Logistic regression (output probability):
y = σ ( W x + b ) = 1 1 + e − ∑ i = 1 n w i x i − b y=\sigma(Wx+b)=\frac{1}{1+e^{-\sum\limits_{i=1}^n{w_ix_i}-b}} y = σ ( W x + b ) = 1 + e − i = 1 ∑ n w i x i − b 1 L = − ∑ i = 1 n y i log ( y ^ i ) L=-\sum\limits_{i=1}^n{y_i\log(\hat{y}_i)} L = − i = 1 ∑ n y i log ( y ^ i )
If model can't even fit training data,
then model have large bias (underfitting).
If model can fit training data but not testing data,
then model have large variance (overfitting).
To prevent underfitting, we can:
Add more features as input.
Use more complex and flexible model.
More complex model does not always lead to better performance
on testing data or new data.
Model Training Error Testing Error x x x 31.9 35.0 x 2 x^2 x 2 15.4 18.4 x 3 x^3 x 3 15.3 18.1 x 4 x^4 x 4 14.9 28.2 x 5 x^5 x 5 12.8 232.1
A extreme example,
such function obtains 0 0 0
f ( x ) = { y i , ∃ x i ∈ X random , otherwise \begin{align*}
f(x)=\begin{cases}
y_i, & \exists{x_i}\in{X} \\
\text{random}, & \text{otherwise}
\end{cases}
\end{align*} f ( x ) = { y i , random , ∃ x i ∈ X otherwise To prevent overfitting, we can:
More training data.
Data augmentation: crop, flip, rotate, cutout, mixup.
Constrained model:
Less parameters, sharing parameters.
Less features.
Early stopping.
Dropout.
Regularization.
L ( w ) = ∑ i = 1 n ( y i − y ^ i ) 2 + λ ∑ i = 1 n w i 2 w t + 1 = w t − η ∇ L ( w ) = w t − η ( ∂ L ∂ w + λ w t ) = ( 1 − η λ ) w t − η ∂ L ∂ w ( Regularization: Weight Decay ) \begin{split}
L(w)&=\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2+\lambda\sum\limits_{i=1}^n{w_i^2}\\
w_{t+1}&=w_t-\eta\nabla{L(w)}\\
&=w_t-\eta(\frac{\partial{L}}{\partial{w}}+\lambda{w_t})\\
&=(1-\eta\lambda)w_t-\eta\frac{\partial{L}}{\partial{w}}
\quad (\text{Regularization: Weight Decay})
\end{split} L ( w ) w t + 1 = i = 1 ∑ n ( y i − y ^ i ) 2 + λ i = 1 ∑ n w i 2 = w t − η ∇ L ( w ) = w t − η ( ∂ w ∂ L + λ w t ) = ( 1 − η λ ) w t − η ∂ w ∂ L ( Regularization: Weight Decay )
Binary classification:
y = δ ( W x + b ) y=\delta(Wx+b) y = δ ( W x + b ) L = ∑ i = 1 n δ ( y i ≠ y ^ i ) L=\sum\limits_{i=1}^n\delta(y_i\ne\hat{y}_i) L = i = 1 ∑ n δ ( y i = y ^ i )
Multi-class classification:
y = softmax ( W x + b ) y=\text{softmax}(Wx+b) y = softmax ( W x + b ) L = − ∑ i = 1 n y i log ( y ^ i ) L=-\sum\limits_{i=1}^n{y_i\log(\hat{y}_i)} L = − i = 1 ∑ n y i log ( y ^ i )
Non-linear model:
Deep learning: y = softmax ( ReLU ( W x + b ) ) y=\text{softmax}(\text{ReLU}(Wx+b)) y = softmax ( ReLU ( W x + b ))
Support vector machine (SVM): y = sign ( W x + b ) y=\text{sign}(Wx+b) y = sign ( W x + b )
Decision tree: y = vote ( leaves ( x ) ) y=\text{vote}(\text{leaves}(x)) y = vote ( leaves ( x ))
K-nearest neighbors (KNN): y = vote ( neighbors ( x ) ) y=\text{vote}(\text{neighbors}(x)) y = vote ( neighbors ( x ))
Find a function F F F
F : X × Y → R F:X\times{Y}\to{R} F : X × Y → R F ( x , y ) F(x, y) F ( x , y ) y y y x x x
Given an object x x x
y ~ = arg max y ∈ Y F ( x , y ) \tilde{y}=\arg\max\limits_{y\in{Y}}F(x, y) y ~ = arg y ∈ Y max F ( x , y )
Evaluation: what does F ( X , y ) F(X, y) F ( X , y )
Inference: how to solve arg max \arg\max arg max
Training: how to find F ( x , y ) F(x, y) F ( x , y )
F ( x , y ) = ∑ i = 1 n w i ϕ i ( x , y ) = [ w 1 w 2 w 3 ⋮ w n ] ⋅ [ ϕ 1 ( x , y ) ϕ 2 ( x , y ) ϕ 3 ( x , y ) ⋮ ϕ n ( x , y ) ] = W ⋅ Φ ( x , y ) \begin{split}
F(x, y)&=\sum\limits_{i=1}^n{w_i\phi_i(x, y)} \\
&=\begin{bmatrix}w_1\\w_2\\w_3\\\vdots\\w_n\end{bmatrix}\cdot
\begin{bmatrix}\phi_1(x, y)\\\phi_2(x, y)\\\phi_3(x, y)\\\vdots\\\phi_n(x, y)\end{bmatrix}\\
&=W\cdot\Phi(x, y)
\end{split} F ( x , y ) = i = 1 ∑ n w i ϕ i ( x , y ) = w 1 w 2 w 3 ⋮ w n ⋅ ϕ 1 ( x , y ) ϕ 2 ( x , y ) ϕ 3 ( x , y ) ⋮ ϕ n ( x , y ) = W ⋅ Φ ( x , y ) 主成分分析 (PCA) 是一种常用的数据降维方法, 将 m m m n n n k k k k k k 1 1 1 0 0 0 k k k
C = 1 m X X T = 1 m [ ∑ i = 1 m ( x i 1 ) 2 ∑ i = 1 m x i 1 x i 2 … ∑ i = 1 m x i 1 x i n ∑ i = 1 m x i 2 x i 1 ∑ i = 1 m ( x i 2 ) 2 … ∑ i = 1 m x i 2 x i n ⋮ ⋮ ⋱ ⋮ ∑ i = 1 m x i n x i 1 ∑ i = 1 m x i n x i 2 … ∑ i = 1 m ( x i n ) 2 ] \begin{equation}
C=\frac{1}{m}XX^T=\frac{1}{m}\begin{bmatrix}
\sum_{i=1}^m(x_i^1)^2&\sum_{i=1}^m{x_i^1x_i^2}&\dots&\sum_{i=1}^m{x_i^1x_i^n}\\
\sum_{i=1}^m{x_i^2x_i^1}&\sum_{i=1}^m(x_i^2)^2&\dots&\sum_{i=1}^m{x_i^2x_i^n}\\
\vdots&\vdots&\ddots&\vdots\\
\sum_{i=1}^m{x_i^nx_i^1}&\sum_{i=1}^m{x_i^nx_i^2}&\dots&\sum_{i=1}^m(x_i^n)^2
\end{bmatrix}
\end{equation} C = m 1 X X T = m 1 ∑ i = 1 m ( x i 1 ) 2 ∑ i = 1 m x i 2 x i 1 ⋮ ∑ i = 1 m x i n x i 1 ∑ i = 1 m x i 1 x i 2 ∑ i = 1 m ( x i 2 ) 2 ⋮ ∑ i = 1 m x i n x i 2 … … ⋱ … ∑ i = 1 m x i 1 x i n ∑ i = 1 m x i 2 x i n ⋮ ∑ i = 1 m ( x i n ) 2 协方差矩阵 C C C i i i j j j j j j i i i i i i j j j
将原始数据按列组成 n n n m m m X X X
将 X X X x ˉ = 0 \bar{x}=0 x ˉ = 0
求出协方差矩阵 C = 1 m X X T C=\frac{1}{m}XX^T C = m 1 X X T
将特征向量按对应特征值大小从上到下按行排列成矩阵, 取前 k k k P P P
Y = P X Y=PX Y = PX k k k
x i ′ = x i − μ σ x'_i=\frac{x_i-\mu}{\sigma} x i ′ = σ x i − μ 词嵌入是自然语言处理 (NLP) 中的一种技术,
将词汇映射到实数向量空间, 使得词汇之间的语义关系可以通过向量空间中的距离来表示.
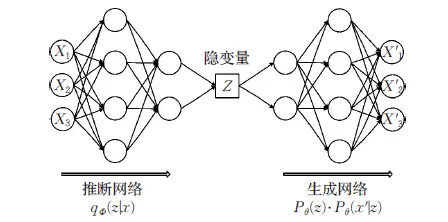
变分自编码器 (VAEs) 是一种生成模型, 通过学习数据的潜在分布来生成新的数据:
Z = Encoder ( X ) X ′ = Decoder ( Z ) L = Min Loss ( X ′ , X ) \begin{split}
Z&=\text{Encoder}(X) \\
X'&=\text{Decoder}(Z) \\
L&=\text{Min Loss}(X',X)
\end{split} Z X ′ L = Encoder ( X ) = Decoder ( Z ) = Min Loss ( X ′ , X ) 变分自动编码器学习的是隐变量 (特征) Z Z Z z ∼ N ( 0 , I ) , x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) z\sim N(0, I), x|z\sim N\big(\mu(z), \sigma(z)\big) z ∼ N ( 0 , I ) , x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) q ( z ∣ x ) q(z|x) q ( z ∣ x ) q q q p ( z ∣ x ) p(z|x) p ( z ∣ x )
Feature disentangle:
voice conversion.
Discrete representation:
unsupervised classification, unsupervised summarization.
Anomaly detection:
face detection, fraud detection, disease detection, network intrusion detection.
Compression and decompression.
Generator.
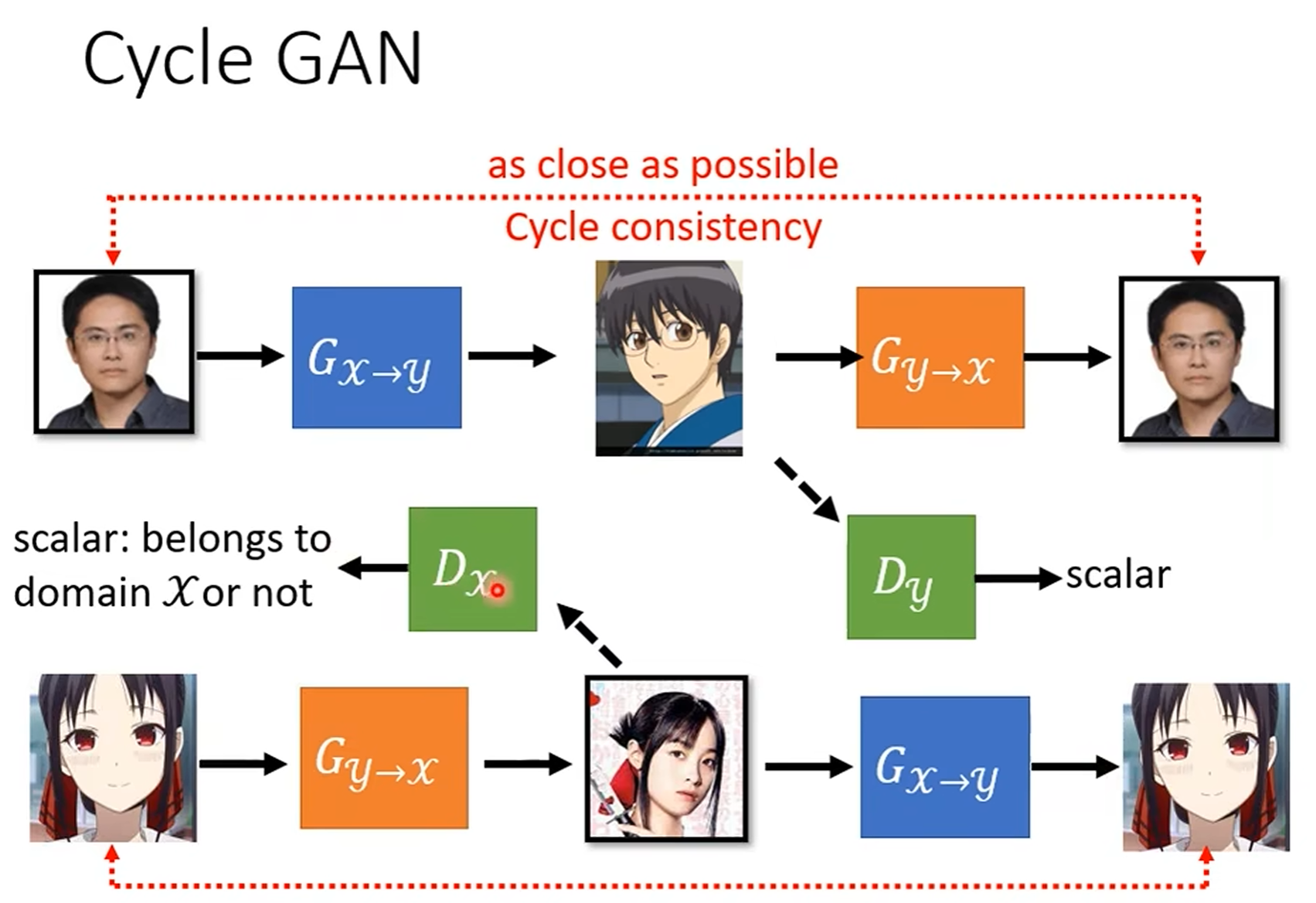
生成对抗网络 (GANs) 由两个网络组成: 生成器 (Generator) 和判别器 (Discriminator).
生成器的目标是生成尽可能逼真的数据, 判别器的目标是尽可能准确地区分真实数据和生成数据.
两个网络相互对抗, 生成器生成数据 (decoder in VAE), 判别器判断数据真伪 (1 / 0 1/0 1/0
G ∗ = arg min G max D V ( G , D ) D ∗ = arg max D V ( D , G ) \begin{split}
G^*&=\arg\min_G\max_DV(G,D)\\
D^*&=\arg\max_DV(D,G)
\end{split} G ∗ D ∗ = arg G min D max V ( G , D ) = arg D max V ( D , G )
Pre-trained models + fine-tuning (downstream tasks):
Cross lingual.
Cross discipline.
Pre-training with artificial data.
Long context window.
Content filtering: 去除有害内容.
Text extraction: 去除 HTML 标签.
Quality filtering: 去除低质量内容.
Document deduplication: 去除重复内容.
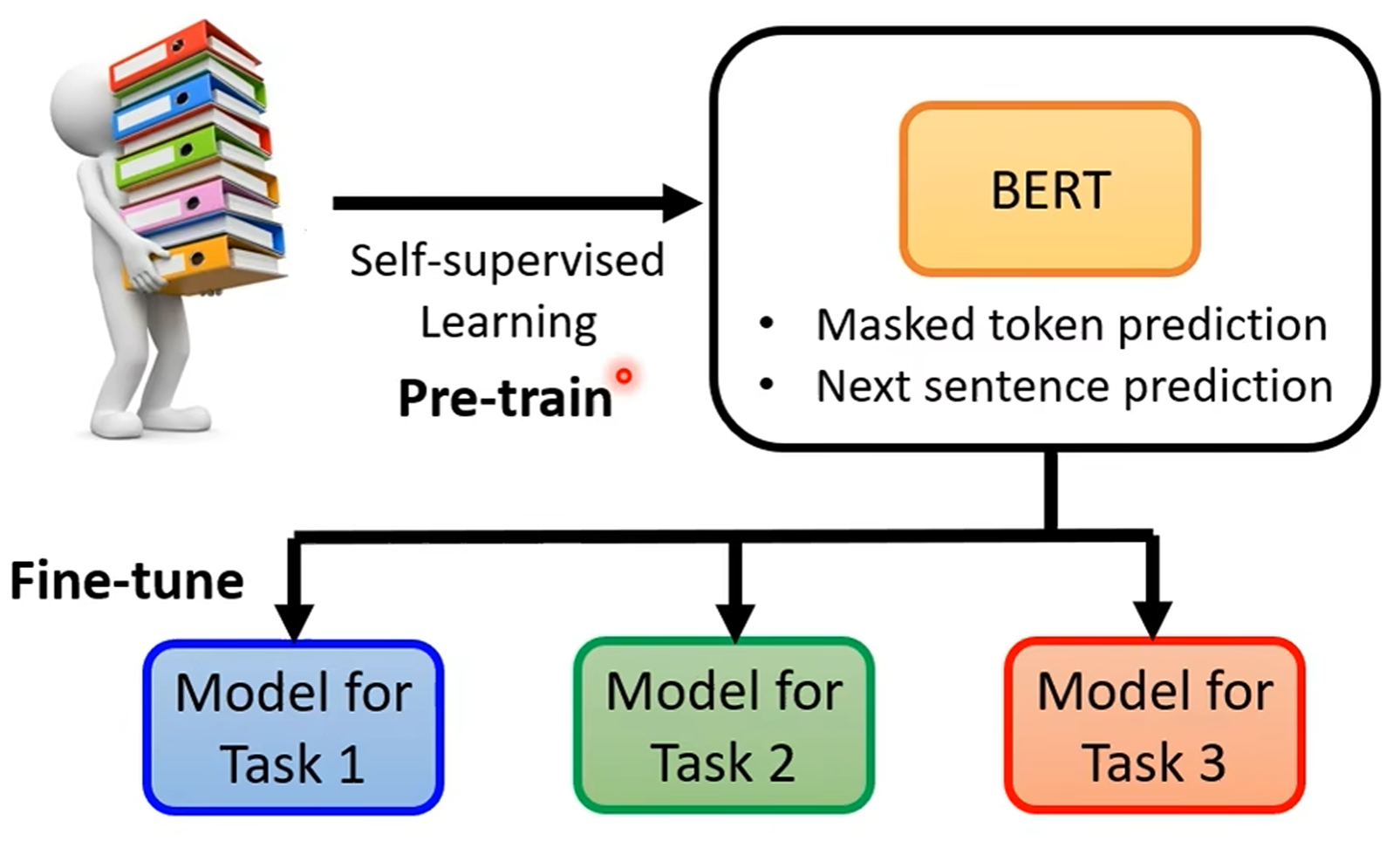
BERT (Bidirectional Encoder Representations from Transformers) 是一种 Encoder-only 预训练模型,
通过大规模无监督学习, 学习文本的语义信息, 用于下游任务的微调:
Masked token prediction: 随机遮挡输入文本中的一些词, 预测被遮挡的词.
Next sentence prediction: 预测两个句子的顺序关系.
GPT (Generative Pre-trained Transformers) 是一种 Decoder-only 预训练模型.
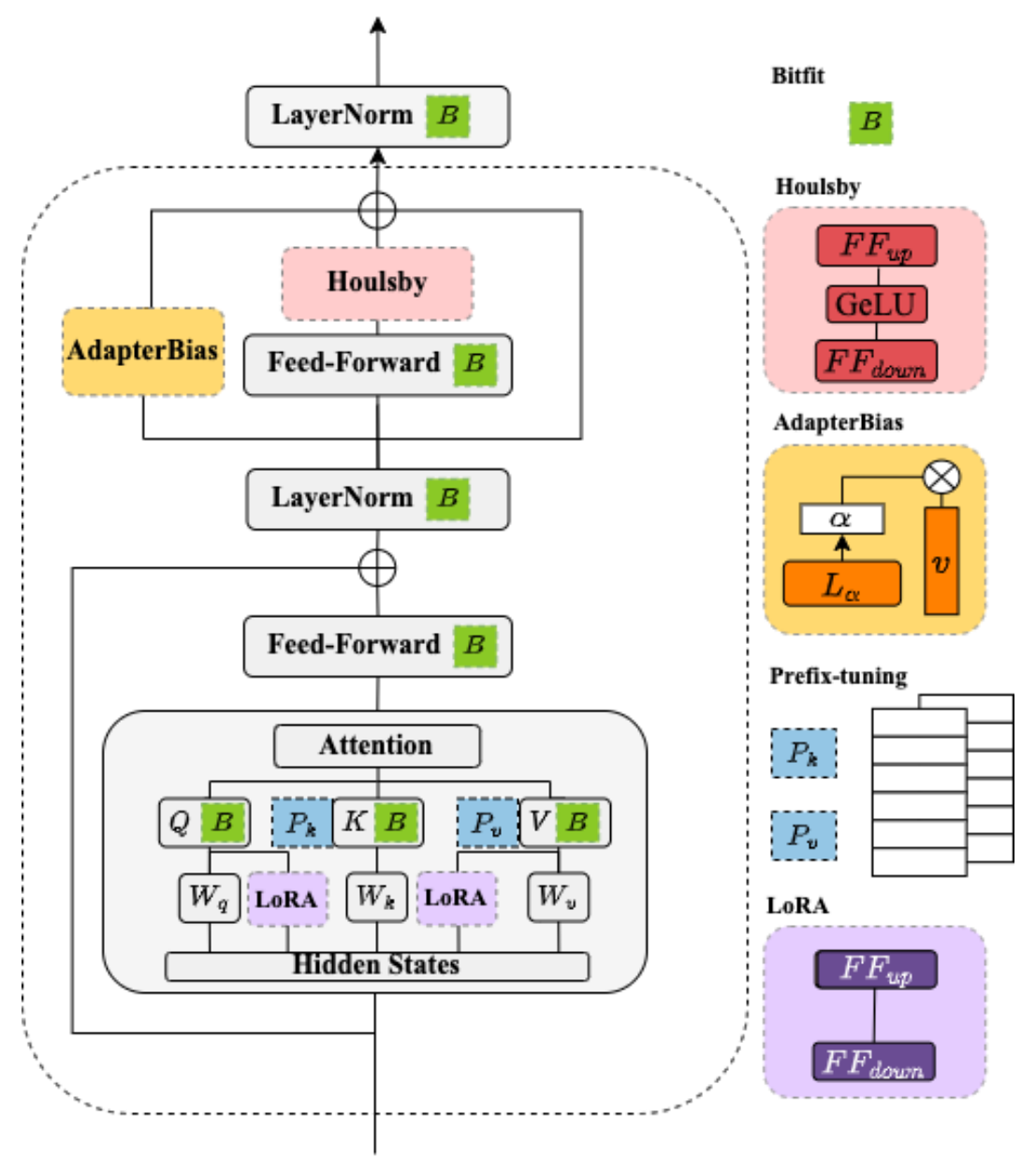
低秩适配 (LoRA) 是一种参数高效微调技术 (Parameter-efficient Fine-tuning),
其基本思想是冻结原始矩阵 W 0 ∈ R H × H W_0\in\mathbb{R}^{H\times{H}} W 0 ∈ R H × H A ∈ R H × R A\in\mathbb{R}^{H\times{R}} A ∈ R H × R B ∈ R H × R B\in\mathbb{R}^{H\times{R}} B ∈ R H × R Δ W = A ⋅ B T \Delta{W}=A\cdot{B^T} Δ W = A ⋅ B T R ≪ H R\ll{H} R ≪ H
W = W 0 + Δ W = W 0 + A ⋅ B T \begin{equation}
W=W_0+\Delta{W}=W_0+A\cdot{B^T}
\end{equation} W = W 0 + Δ W = W 0 + A ⋅ B T 在微调期间, 原始的矩阵参数 W 0 W_0 W 0 A A A B B B
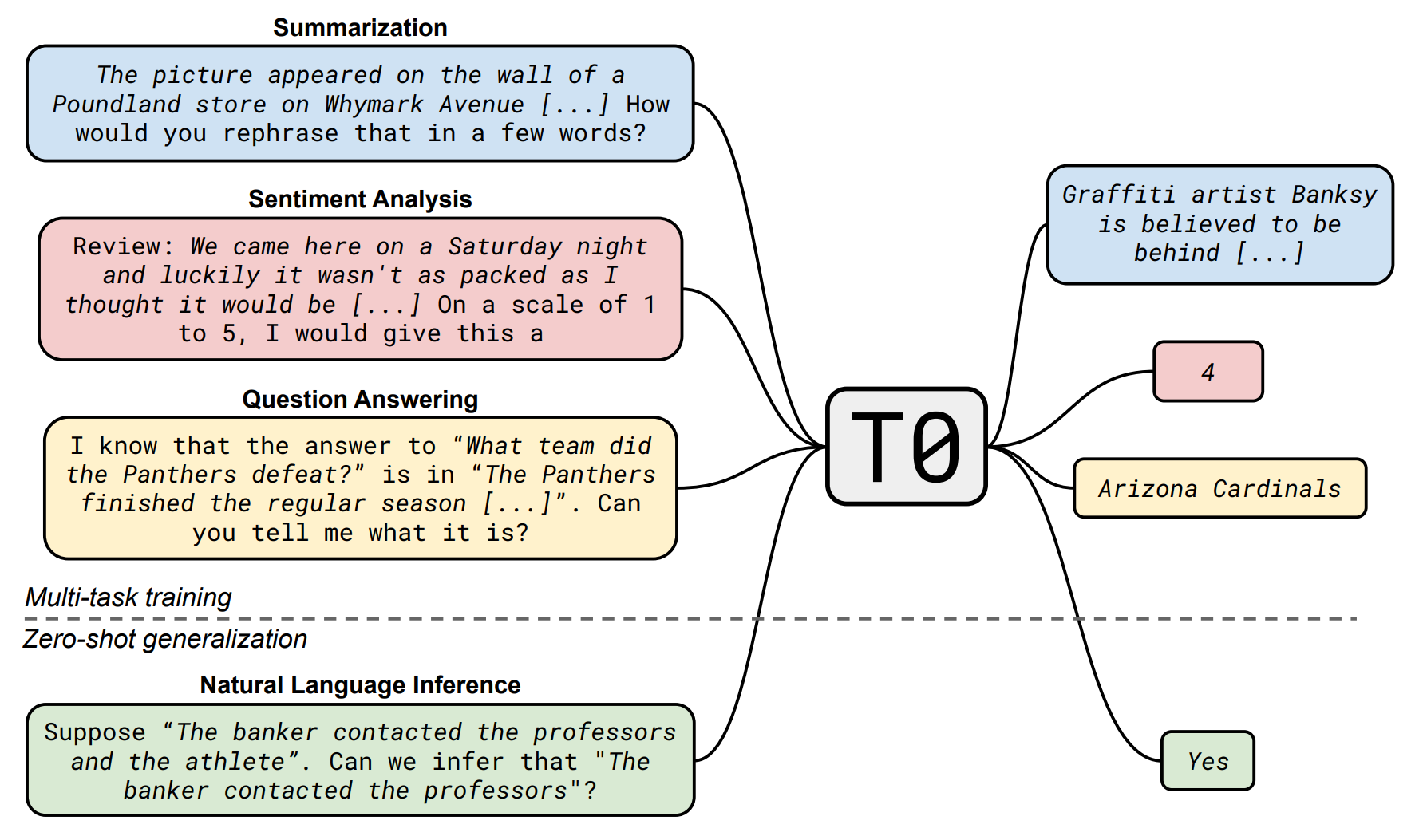
Make model can understand human instructions not appear in training data:
提高指令复杂性和多样性能够促进模型性能的提升.
更大的参数规模有助于提升模型的指令遵循能力.
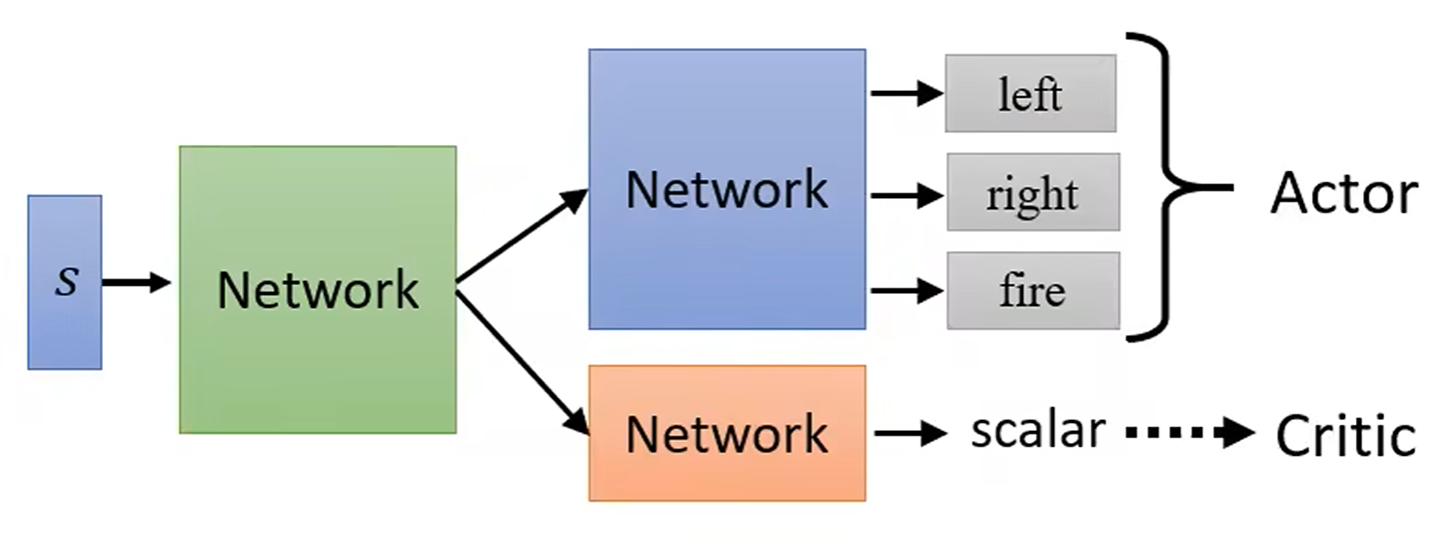
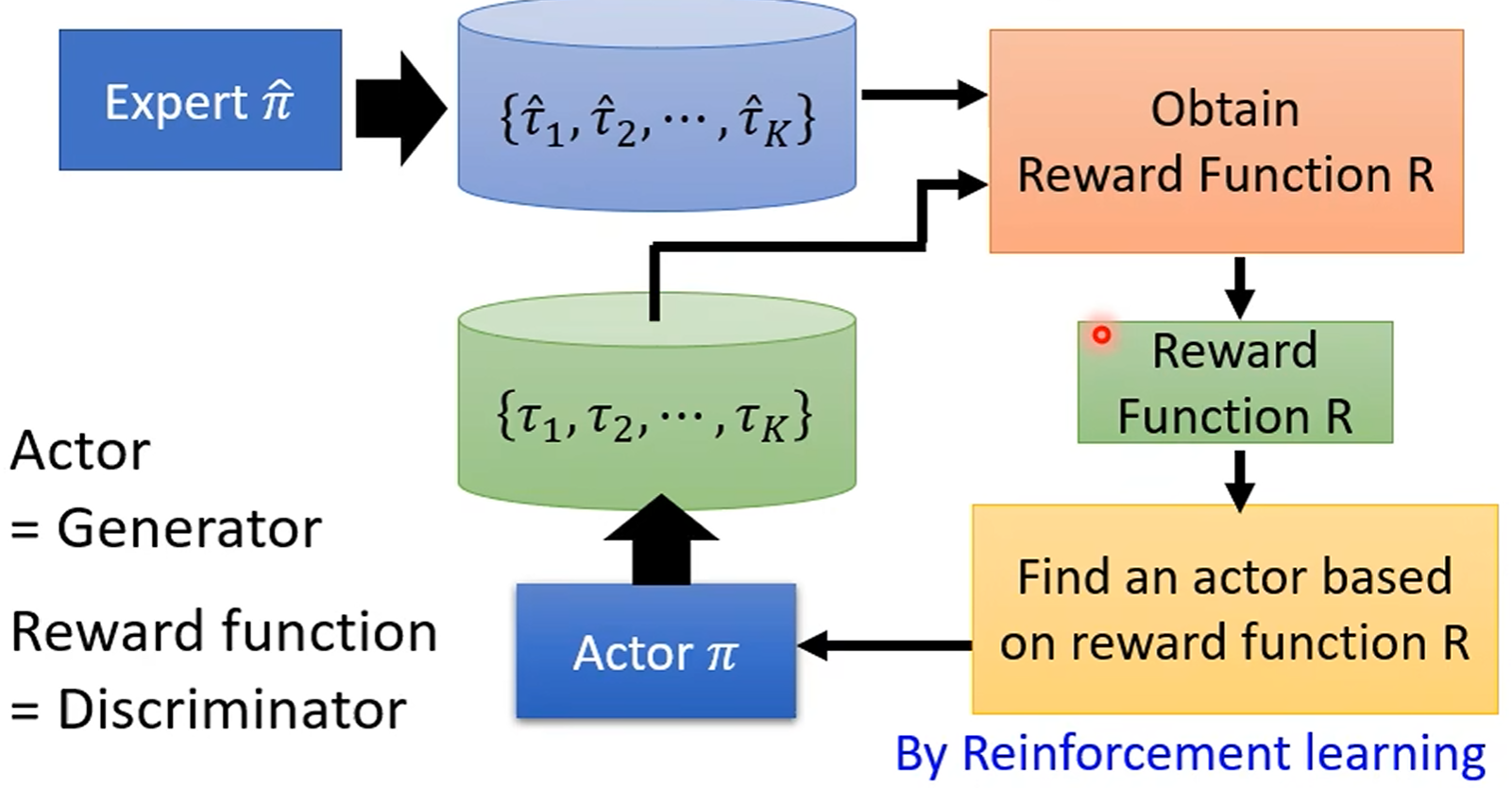
强化学习是一种机器学习方法, 通过智能体与环境交互,
智能体根据环境的反馈调整策略, 利用梯度上升算法 (Gradient Ascent),
最大化长期奖励 (learn from rewards and mistakes).
θ ∗ = arg max θ R ˉ θ = arg max θ ∑ τ R ( τ ) P ( τ ∣ θ ) θ t + 1 = θ t + η ∇ R ˉ θ ∇ R ˉ θ = [ ∂ R ˉ θ ∂ w 1 ∂ R ˉ θ ∂ w 2 ⋮ ∂ R ˉ θ ∂ b 1 ⋮ ] R t = ∑ n = t N γ n − t r n \begin{equation}
\begin{split}
\theta^*&=\arg\max\limits_\theta\bar{R}_\theta=\arg\max\limits_\theta\sum\limits_{\tau}R(\tau)P(\tau|\theta)\\
\theta_{t+1}&=\theta_t+\eta\nabla\bar{R}_\theta\\
\nabla\bar{R}_\theta&=\begin{bmatrix}\frac{\partial\bar{R}_\theta}{\partial{w_1}}\\\frac{\partial\bar{R}_\theta}{\partial{w_2}}\\\vdots\\\frac{\partial\bar{R}_\theta}{\partial{b_1}}\\\vdots\end{bmatrix}\\
R_t&=\sum\limits_{n=t}^N\gamma^{n-t}r_n
\end{split}
\end{equation} θ ∗ θ t + 1 ∇ R ˉ θ R t = arg θ max R ˉ θ = arg θ max τ ∑ R ( τ ) P ( τ ∣ θ ) = θ t + η ∇ R ˉ θ = ∂ w 1 ∂ R ˉ θ ∂ w 2 ∂ R ˉ θ ⋮ ∂ b 1 ∂ R ˉ θ ⋮ = n = t ∑ N γ n − t r n