Skip to main content

Mathematical Analysis

Limit​

洛必达法则是求解分数形式的未定型极限 lim⁡x→a00\lim_{x\to{a}}\frac{0}{0} 的有效方法之一:

lim⁡x→af(x)g(x)=lim⁡x→adf(x)dg(x)=lim⁡x→adfdx(a)dxdgdx(a)dx=lim⁡x→adfdx(a)dgdx(a)=lim⁡x→af′(a)g′(a)\begin{equation} \begin{split} \lim_{x\to{a}}\frac{f(x)}{g(x)} &=\lim_{x\to{a}}\frac{df(x)}{dg(x)} \\ &=\lim_{x\to{a}}\frac{\frac{df}{dx}(a)dx}{\frac{dg}{dx}(a)dx} \\ &=\lim_{x\to{a}}\frac{\frac{df}{dx}(a)}{\frac{dg}{dx}(a)} \\ &=\lim_{x\to{a}}\frac{f'(a)}{g'(a)} \end{split} \end{equation}

Derivative​

常见导数:

ddxxn=nxn−1ddxsin⁡x=cos⁡xddxcos⁡x=−sin⁡xddxax=axln⁡addxex=exddxlog⁡ax=1xln⁡addxln⁡x=1xddx(g(x)+h(x))=g′(x)+h′(x)ddx(g(x)h(x))=g′(x)h(x)+g(x)h′(x)ddxf(g(x))=f′(g(x))g′(x)ddxf−1(x)=1f′(f−1(x))ddx∫a(x)b(x)f(t)dt=f(b(x))b′(x)−f(a(x))a′(x)\begin{equation} \begin{split} \frac{d}{dx}x^n&=nx^{n-1} \\ \frac{d}{dx}\sin{x}&=\cos{x} \\ \frac{d}{dx}\cos{x}&=-\sin{x} \\ \frac{d}{dx}a^x&=a^x\ln{a} \\ \frac{d}{dx}e^x&=e^x \\ \frac{d}{dx}\log_a{x}&=\frac{1}{x\ln{a}} \\ \frac{d}{dx}\ln{x}&=\frac{1}{x} \\ \frac{d}{dx}(g(x)+h(x))&=g'(x)+h'(x) \\ \frac{d}{dx}(g(x)h(x))&=g'(x)h(x)+g(x)h'(x) \\ \frac{d}{dx}f(g(x))&=f'(g(x))g'(x) \\ \frac{d}{dx}f^{-1}(x)&=\frac{1}{f'(f^{-1}(x))} \\ \frac{d}{dx}\int_{a(x)}^{b(x)}f(t)dt&=f(b(x))b'(x)-f(a(x))a'(x) \end{split} \end{equation}

Series​

泰勒级数利用函数在某点的各阶导数, 近似该点附近函数的值:

11−x=∑n=0∞xn∣x∣<1ex=∑n=0∞xnn!ln⁡(1+x)=∑n=1∞(−1)n−1nxnx∈(−1,1]sin⁡(x)=∑n=0∞(−1)n(2n+1)!x2n+1cos⁡(x)=∑n=0∞(−1)n(2n)!x2nf(x)=∑n=0∞f(n)(x0)n!(x−x0)n=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+…\begin{equation} \begin{split} \frac{1}{1-x}&=\sum\limits_{n=0}^{\infty}x^n \quad |x|\lt1 \\ e^x&=\sum\limits_{n=0}^{\infty}\frac{x^n}{n!} \\ \ln(1+x)&=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}x^n \quad x\in(-1,1] \\ \sin(x)&=\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1} \\ \cos(x)&=\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}x^{2n} \\ f(x)&=\sum\limits_{n=0}^{\infty}\frac{f^{(n)(x_0)}}{n!}(x-x_0)^n \\ &=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dots \end{split} \end{equation}

Euler's Formula​

复数平面 (Complex Plane) 上的圆周运动:

eix=cos⁡x+isin⁡x\begin{equation} e^{ix}=\cos{x}+i\sin{x} \end{equation}

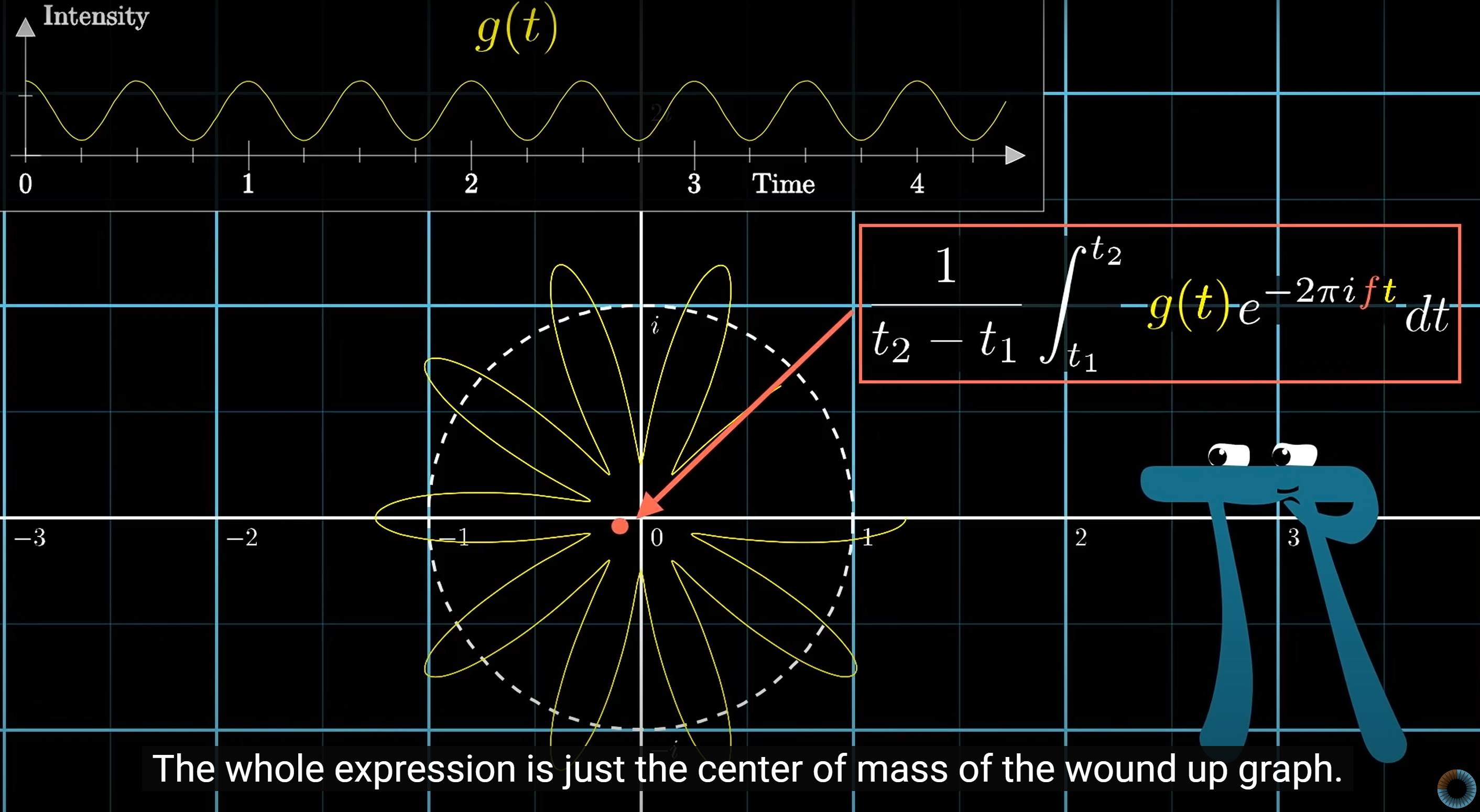
Fourier Transform​

Time to frequency transform:

f^(ξ)=∫−∞∞f(t)e−2πiξtdt\begin{equation} \hat{f}(\xi)=\int_{-\infty}^{\infty}f(t)e^{-2\pi i\xi t}dt \end{equation}

Discrete Fourier Transform (DFT):

X[k]=∑n=0N−1xne−i2πNkn\begin{equation} X[k]=\sum\limits_{n=0}^{N-1}x_n e^{-\frac{i2\pi}{N}kn} \end{equation}

outcomes

[111…11e2πine2πi(2)n…e2πi(n−1)n1e2πi(2)ne2πi(4)n…e2πi(2)(n−1)n⋮⋮⋮⋱⋮1e2πi(n−1)ne2πi(2)(n−1)n…e2πi(n−1)(n−1)n]\begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & e^{\frac{2\pi i}{n}} & e^{\frac{2\pi i(2)}{n}} & \dots & e^{\frac{2\pi i(n-1)}{n}} \\ 1 & e^{\frac{2\pi i(2)}{n}} & e^{\frac{2\pi i(4)}{n}} & \dots & e^{\frac{2\pi i(2)(n-1)}{n}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & e^{\frac{2\pi i(n-1)}{n}} & e^{\frac{2\pi i(2)(n-1)}{n}} & \dots & e^{\frac{2\pi i(n-1)(n-1)}{n}} \end{bmatrix}

Fourier Transform

Differential Equation​

微分方程 (Differential Equation) 是描述变量之间关系的方程, 通常包含未知函数及其导数, 用于描述物理现象和自然规律.

First Order Differential Equation​

一阶微分方程:

ddt[x(t)y(t)]=[abcd][x(t)y(t)]⇒[x(t)y(t)]=e[abcd]t[x(0)y(0)]\begin{equation} \frac{d}{dt}\begin{bmatrix}x(t)\\y(t)\end{bmatrix} =\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}x(t)\\y(t)\end{bmatrix} \Rightarrow \begin{bmatrix}x(t)\\y(t)\end{bmatrix} =e^{\begin{bmatrix}a&b\\c&d\end{bmatrix}t}\begin{bmatrix}x(0)\\y(0)\end{bmatrix} \end{equation} ifv⃗(t)=eMtv⃗0thenddtv⃗(t)=ddteMtv⃗0=ddt∑n=0∞Mnn!tnv⃗0=∑n=0∞Mnn!ntn−1v⃗0=M∑n=0∞Mn−1(n−1)!tn−1v⃗0=MeMtv⃗0=Mv⃗(t)\begin{split} \text{if} \quad \vec{v}(t)&=e^{Mt}\vec{v}_0 \\ \text{then} \quad \frac{d}{dt}\vec{v}(t) &=\frac{d}{dt}e^{Mt}\vec{v}_0 \\ &=\frac{d}{dt}\sum\limits_{n=0}^{\infty}\frac{M^n}{n!}t^n\vec{v}_0 \\ &=\sum\limits_{n=0}^{\infty}\frac{M^n}{n!}nt^{n-1}\vec{v}_0 \\ &=M\sum\limits_{n=0}^{\infty}\frac{M^{n-1}}{(n-1)!}t^{n-1}\vec{v}_0 \\ &=Me^{Mt}\vec{v}_0 \\ &=M\vec{v}(t) \end{split}

Second Order Differential Equation​

x¨(t)=−μx˙(t)−ωx(t)\begin{equation} \ddot{x}(t)=-\mu\dot{x}(t)-\omega x(t) \end{equation}

Gravitational force equation:

y¨(t)=−g,y˙(t)=−gt+v0dx⃗1dt=v⃗1,dv⃗1dt=Gm2(x⃗2−x⃗1∥x⃗2−x⃗1∥)(1∥x⃗2−x⃗1∥2)θ¨(t)=−μθ˙(t)−gLsin⁡(θ(t))\begin{split} \ddot{y}(t)=-g, \quad & \dot{y}(t)=-gt+v_0 \\ \frac{d\vec{x}_1}{dt}=\vec{v}_1, \quad & \frac{d\vec{v}_1}{dt}=Gm_2\Big(\frac{\vec{x}_2-\vec{x}_1}{\|\vec{x}_2-\vec{x}_1\|}\Big)\Big(\frac{1}{\|\vec{x}_2-\vec{x}_1\|^2}\Big) \\ & \ddot{\theta}(t)=-\mu\dot{\theta}(t)-\frac{g}{L}\sin\big({\theta}(t)\big) \end{split}

Partial Differential Equation​

热传导方程:

∂T∂t(x,t)=α∂2T∂x2(x,t)\frac{\partial{T}}{\partial{t}}(x,t)=\alpha\frac{\partial^2{T}}{\partial{x^2}}(x,t)

Black-Scholes / Merton equation:

∂V∂t+rS∂V∂S+12σ2S2∂2V∂S2−rV=0\frac{\partial{V}}{\partial{t}}+rS\frac{\partial{V}}{\partial{S}}+\frac{1}{2}\sigma^2S^2\frac{\partial^2{V}}{\partial{S^2}}-rV=0

Phase Space​

相空间是描述系统状态的空间, 每个点代表系统的一个状态, 点的轨迹描述了系统的演化.

import numpy as np

# Physical constants
g = 9.8
L = 2
mu = 0.1

THETA_0 = np.pi / 3  # 60 degrees
THETA_DOT_0 = 0  # No initial angular velocity

# Definition of ODE
def get_theta_double_dot(theta, theta_dot):
    return -mu * theta_dot - (g / L) * np.sin(theta)

# Solution to the differential equation (numerically)
def theta(t):
    theta = THETA_0
    theta_dot = THETA_DOT_0
    delta_t = 0.01  # Time step
    for _ in np.arange(0, t, delta_t):
        theta_double_dot = get_theta_double_dot(theta, theta_dot)
        theta += theta_dot * delta_t
        theta_dot += theta_double_dot * delta_t
    return theta