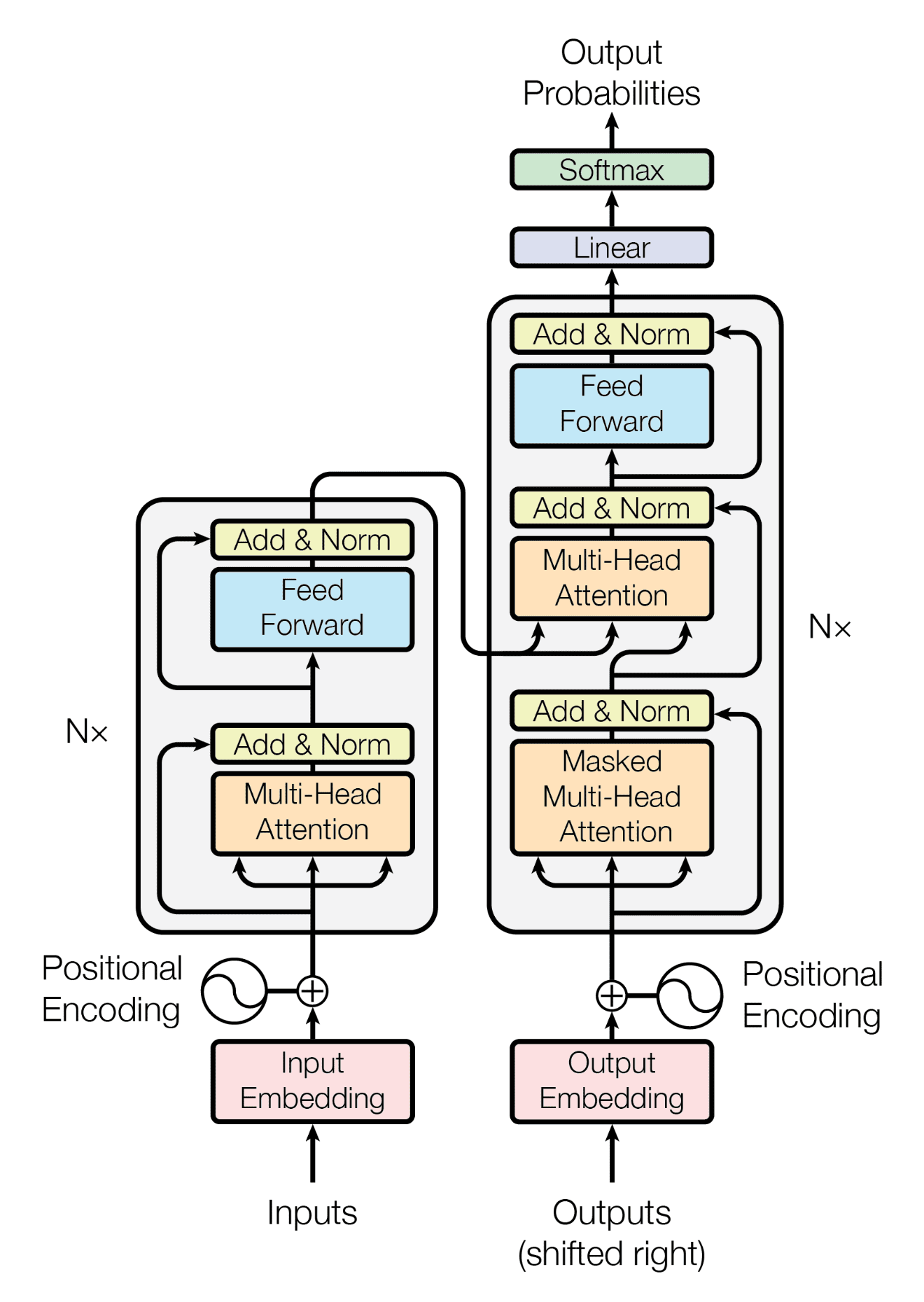
Transformer

• Self-attention only: comparing to Recurrent Neural Networks (RNNs), no recurrent layers, allows for more parallelization.
• Multi-headed attention: consistent with Convolutional Neural Networks (CNNs), multiple output channels.

Self-Attention Mechanism

In layman's terms, a self-attention module takes in n inputs and returns n outputs:

• Self: allows the inputs to interact with each other
• Attention: find out who they should pay more attention to.
• The outputs are aggregates of these interactions and attention scores.

$$\begin{equation} \text{Attention}(Q, K, V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V \end{equation}$$

The illustrations are divided into the following steps:

• Prepare inputs.
• Weights initialization (Constant/Random/Xavier/Kaiming Initialization).
• Derive query, key and value.
• Calculate attention scores for input.
• Calculate softmax.
• Multiply scores with values.
• Sum weighted values to get output.

$$X=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} =\begin{bmatrix}1&0&1&0\\0&2&0&2\\1&1&1&1\end{bmatrix}$$

Weights for query, key and value (these weights are usually small numbers, initialized randomly using an appropriate random distribution like Gaussian, Xavier and Kaiming distributions):

$$W_Q=\begin{bmatrix}q_1&q_2&q_3\end{bmatrix} =\begin{bmatrix}1&0&1\\1&0&0\\0&0&1\\0&1&1\end{bmatrix}$$ $$W_K=\begin{bmatrix}k_1&k_2&k_3\end{bmatrix} =\begin{bmatrix}0&0&1\\1&1&0\\0&1&0\\1&1&0\end{bmatrix}$$ $$W_V=\begin{bmatrix}v_1&v_2&v_3\end{bmatrix} =\begin{bmatrix}0&2&0\\0&3&0\\1&0&3\\1&1&0\end{bmatrix}$$

Derive query, key and value:

$$Q=XW_Q =\begin{bmatrix}1&0&1&0\\0&2&0&2\\1&1&1&1\end{bmatrix} \begin{bmatrix}1&0&1\\1&0&0\\0&0&1\\0&1&1\end{bmatrix} =\begin{bmatrix}1&0&2\\2&2&2\\2&1&3\end{bmatrix}$$ $$K=XW_K =\begin{bmatrix}1&0&1&0\\0&2&0&2\\1&1&1&1\end{bmatrix} \begin{bmatrix}0&0&1\\1&1&0\\0&1&0\\1&1&0\end{bmatrix} =\begin{bmatrix}0&1&1\\4&4&0\\2&3&1\end{bmatrix}$$ $$V=XW_V =\begin{bmatrix}1&0&1&0\\0&2&0&2\\1&1&1&1\end{bmatrix} \begin{bmatrix}0&2&0\\0&3&0\\1&0&3\\1&1&0\end{bmatrix} =\begin{bmatrix}1&2&3\\2&8&0\\2&6&3\end{bmatrix}$$

Calculate attention scores $QK^T$ for input:

$$QK^T =\begin{bmatrix}1&0&2\\2&2&2\\2&1&3\end{bmatrix} \begin{bmatrix}0&4&2\\1&4&3\\1&0&1\end{bmatrix} =\begin{bmatrix}2&4&4\\4&16&12\\4&12&10\end{bmatrix}$$

$XX^T$

$XX^T$ 为行向量分别与自己和其他两个行向量做内积 (点乘), 向量的内积表征两个向量的夹角 ($\cos\theta=\frac{a\cdot{b}}{|a||b|}$), 表征一个向量在另一个向量上的投影, 投影的值大, 说明两个向量相关度高 (Relevance/Similarity).

$$\begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ \vdots \\ v_n \end{bmatrix} \cdot \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ \vdots \\ w_n \end{bmatrix} =v_1w_1+v_2w_2+v_3w_3+\dots+v_nw_n$$

Softmaxed attention scores $\text{softmax}(\frac{QK^T}{\sqrt{d_k}})$:

$$\text{softmax}(QK^T) =\text{softmax}\Bigg(\begin{bmatrix}2&4&4\\4&16&12\\4&12&10\end{bmatrix}\Bigg) =\begin{bmatrix}0.0&0.5&0.5\\0.0&1.0&0.0\\0.0&0.9&0.1\end{bmatrix}$$

Softmax

softmax function:

$$\begin{equation} \sigma(z_i)=\frac{e^{z_i/T}}{\sum_{j=1}^K{e^{z_j/T}}} \end{equation}$$

其中, $T$ 为温度参数 (Temperature Parameter), 用于控制 softmax 函数的输出分布的陡峭程度:

• $T=1$ 时, softmax 函数退化为标准形式.
• $T>1$ 时, softmax 函数输出分布更加平缓.
• $T<1$ 时, softmax 函数输出分布更加陡峭.
• $T\to0$ 时, softmax 函数退化为 argmax 函数, 输出分布中只有一个元素为 1, 其他元素为 0.

$\sqrt{d_k}$

矩阵 $A$ 中每一个元素除以 $\sqrt{d_k}$ 后, 方差变为 1. 这使得 $\text{softmax}(A)$ 的分布"陡峭"程度与 $d_k$ 解耦, 从而使得训练过程中梯度值保持稳定.

Alignment vectors (yellow vectors) addition to output:

$$\begin{split} y_1&=\sum\limits_{i=1}^{3}\alpha_{1i}v_i \\ &=\alpha_{11}v_1+\alpha_{12}v_2+\alpha_{13}v_3 \\ &=0.0\begin{bmatrix}1&2&3\end{bmatrix} +0.5\begin{bmatrix}2&8&0\end{bmatrix} +0.5\begin{bmatrix}2&6&3\end{bmatrix} \\ &=\begin{bmatrix}2.0&7.0&1.5\end{bmatrix} \end{split}$$

Repeat for every input:

$$y_2=\begin{bmatrix}2.0&8.0&0.0\end{bmatrix}, y_3=\begin{bmatrix}2.0&7.8&0.3\end{bmatrix}$$

Calculate $\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$ by matrix multiplication:

$$\text{softmax}(QK^T)V =\begin{bmatrix}0.0&0.5&0.5\\0.0&1.0&0.0\\0.0&0.9&0.1\end{bmatrix} \begin{bmatrix}1&2&3\\2&8&0\\2&6&3\end{bmatrix} =\begin{bmatrix}2.0&7.0&1.5\\2.0&8.0&0.0\\2.0&7.8&0.3\end{bmatrix}$$

$QK^TV$

Self-attention 中的 $QKV$ 思想, 另一个层面是想要构建一个具有全局语义 (Context) 整合功能的数据库, 使得 Context Size 内的每个元素都能够看到其他元素的信息, 从而能够更好地进行决策.

import torch
from torch.nn.functional import softmax

# 1. Prepare inputs
x = [
    [1, 0, 1, 0],  # Input 1
    [0, 2, 0, 2],  # Input 2
    [1, 1, 1, 1],  # Input 3
]
x = torch.tensor(x, dtype=torch.float32)

# 2. Weights initialization
w_query = [
    [1, 0, 1],
    [1, 0, 0],
    [0, 0, 1],
    [0, 1, 1],
]
w_key = [
    [0, 0, 1],
    [1, 1, 0],
    [0, 1, 0],
    [1, 1, 0],
]
w_value = [
    [0, 2, 0],
    [0, 3, 0],
    [1, 0, 3],
    [1, 1, 0],
]
w_query = torch.tensor(w_query, dtype=torch.float32)
w_key = torch.tensor(w_key, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)

# 3. Derive query, key and value
queries = x @ w_query
keys = x @ w_key
values = x @ w_value

# 4. Calculate attention scores
attn_scores = queries @ keys.T

# 5. Calculate softmax
attn_scores_softmax = softmax(attn_scores, dim=-1)
# tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
#         [6.0337e-06, 9.8201e-01, 1.7986e-02],
#         [2.9539e-04, 8.8054e-01, 1.1917e-01]])
# For readability, approximate the above as follows
attn_scores_softmax = [
    [0.0, 0.5, 0.5],
    [0.0, 1.0, 0.0],
    [0.0, 0.9, 0.1],
]
attn_scores_softmax = torch.tensor(attn_scores_softmax)

# 6. Multiply scores with values
weighted_values = values[:, None] * attn_scores_softmax.T[:, :, None]

# 7. Sum weighted values
outputs = weighted_values.sum(dim=0)

print(outputs)
# tensor([[2.0000, 7.0000, 1.5000],
#         [2.0000, 8.0000, 0.0000],
#         [2.0000, 7.8000, 0.3000]])
# tensor([[1.9366, 6.6831, 1.5951],
#         [2.0000, 7.9640, 0.0540],
#         [1.9997, 7.7599, 0.3584]])

自注意力机制能够直接建模序列中任意两个位置之间的关系, 进而有效捕获长程依赖关系, 具有更强的序列建模能力. 自注意力的计算过程对于基于硬件的并行优化 (GPU/TPU) 非常友好, 因此能够支持大规模参数的高效优化.

Multi-Head Attention Mechanism

Multiple output channels:

$$\begin{equation} \begin{split} \text{MultiHead}(Q,K,V)&=\text{Concat}(\text{head}_1,\ldots,\text{head}_h)W^O \\ \text{where}\ \text{head}_i&=\text{Attention}(QW_i^Q,KW_i^K,VW_i^V) \end{split} \end{equation}$$

from math import sqrt
import torch
import torch.nn

class Self_Attention(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self, input_dim, dim_k, dim_v):
        super(Self_Attention, self).__init__()
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)
        self._norm_fact = 1 / sqrt(dim_k)

    def forward(self, x):
        Q = self.q(x)  # Q: batch_size * seq_len * dim_k
        K = self.k(x)  # K: batch_size * seq_len * dim_k
        V = self.v(x)  # V: batch_size * seq_len * dim_v

        # Q * K.T() # batch_size * seq_len * seq_len
        attention = nn.Softmax(dim=-1)(torch.bmm(Q, K.permute(0, 2, 1))) * self._norm_fact

        # Q * K.T() * V # batch_size * seq_len * dim_v
        output = torch.bmm(attention, V)

        return output

class Self_Attention_Multiple_Head(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self, input_dim, dim_k, dim_v, nums_head):
        super(Self_Attention_Multiple_Head, self).__init__()
        assert dim_k % nums_head == 0
        assert dim_v % nums_head == 0
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)

        self.nums_head = nums_head
        self.dim_k = dim_k
        self.dim_v = dim_v
        self._norm_fact = 1 / sqrt(dim_k)

    def forward(self, x):
        Q = self.q(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)
        K = self.k(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)
        V = self.v(x).reshape(-1, x.shape[0], x.shape[1], self.dim_v // self.nums_head)
        print(x.shape)
        print(Q.size())

        # Q * K.T() # batch_size * seq_len * seq_len
        attention = nn.Softmax(dim=-1)(torch.matmul(Q, K.permute(0, 1, 3, 2)))

        # Q * K.T() * V # batch_size * seq_len * dim_v
        output = torch.matmul(attention, V).reshape(x.shape[0], x.shape[1], -1)

        return output

Positional Encoding Mechanism

位置编码 使用正弦和余弦函数的 d 维向量编码方法, 用于在输入序列中表示每个单词的位置信息, 丰富了模型的输入数据, 为其提供位置信息 (把词序信号加到词向量上帮助模型学习这些信息):

• 唯一性 (Unique): 为每个时间步输出一个独一无二的编码.
• 一致性 (Consistent): 不同长度的句子之间, 任何两个时间步之间的距离保持一致.
• 泛化性 (Generalizable): 模型能毫不费力地泛化到更长的句子, 位置编码的值是有界的.
• 确定性 (Deterministic): 位置编码的值是确定性的.

编码函数使用正弦和余弦函数, 其频率沿着向量维度进行减少. 编码向量包含每个频率的正弦和余弦对, 以实现 $\sin(x+k)$ 和 $\cos(x+k)$ 的线性变换, 从而有效地表示相对位置.

For $\vec{p_t}\in\mathbb{R}^d$ (where $d\equiv_2{0}$), then $f:\mathbb{N}\to\mathbb{R}^d$

$$\begin{align} \vec{p_t}^{(i)}=f(t)^{(i)}:= \begin{cases} \sin({\omega_k}\cdot{t}), &\text{if}\ i=2k \\ \cos({\omega_k}\cdot{t}), &\text{if}\ i=2k+1 \end{cases} \end{align}$$

where

$$\omega_k=\frac{1}{10000^{2k/d}}$$

outcomes

$$\vec{p_t} = \begin{bmatrix} \sin({\omega_1}\cdot{t}) \\ \cos({\omega_1}\cdot{t}) \\ \\ \sin({\omega_2}\cdot{t}) \\ \cos({\omega_2}\cdot{t}) \\ \\ \vdots \\ \\ \sin({\omega_{d/2}}\cdot{t}) \\ \cos({\omega_{d/2}}\cdot{t}) \end{bmatrix}_{d\times{1}}$$

KV Cache

Prompt caching 缓存的不是文本是思维状态, 本质是复用 KV 矩阵.