Algorithms Basic Notes
Sorting Algorithms
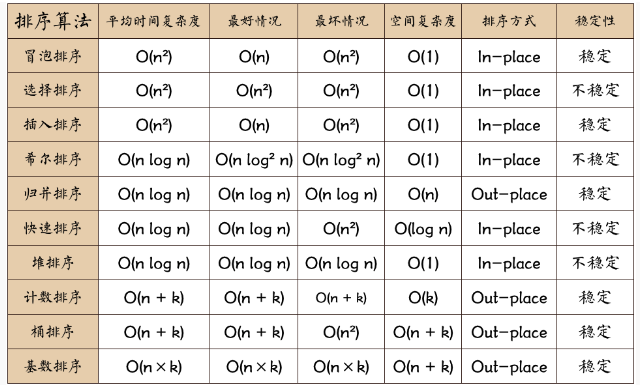
Summary
- 强制稳定: 增加(唯一)时间戳, 修改 CompareTo 接口定义 => 当主元素相同时, 时间戳小的元素更小
Selection Sort
- swap: O(n)
- compare: O(n^2)
Insertion Sort
- swap: O(n^2/4)
- compare: O(n^2/4)
Shell Sort
- swap: O(n^2/4)
- compare: O(n^2/4)
Merge Sort
- 利用 Merge Sort 计算逆序对个数: left[i] > right[j] => inversions += (mid - i + 1), 即所有 i~mid 元素都与 j 元素为逆序对
// merge and count
private static long merge(int[] a, int[] aux, int lo, int mid, int hi) {
long inversions = 0;
// copy to aux[]
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
// merge back to a[]
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (aux[j] < aux[i]) { a[k] = aux[j++]; inversions += (mid -
i + 1); }
else a[k] = aux[i++];
}
return inversions;
}
// return the number of inversions in the subArray b[lo..hi]
// side effect b[lo..hi] is rearranged in ascending order
private static long count(int[] a, int[] b, int[] aux, int lo, int hi) {
long inversions = 0;
if (hi <= lo) return 0;
int mid = lo + (hi - lo) / 2;
inversions += count(a, b, aux, lo, mid);
inversions += count(a, b, aux, mid+1, hi);
inversions += merge(b, aux, lo, mid, hi);
assert inversions == brute(a, lo, hi);
return inversions;
}
/**
* Returns the number of inversions in the integer array.
* The argument array is not modified.
* @param a the array
* @return the number of inversions in the array. An inversion is a pair of
* indices {@code i} and {@code j} such that {@code i < j}
* and {@code a[i]} > {@code a[j]}.
*/
public static long count(int[] a) {
int[] b = new int[a.length];
int[] aux = new int[a.length];
for (int i = 0; i < a.length; i++)
b[i] = a[i];
long inversions = count(a, b, aux, 0, a.length - 1);
return inversions;
}
// return Kendall tau distance between two permutations
public static long distance(int[] a, int[] b) {
if (a.length != b.length) {
throw new IllegalArgumentException("Array dimensions disagree");
}
int n = a.length;
int[] ainV = new int[n];
for (int i = 0; i < n; i++)
ainV[a[i]] = i;
Integer[] bNew = new Integer[n];
for (int i = 0; i < n; i++)
bNew[i] = ainV[b[i]];
return Inversions.count(bNew);
}
Quick Sort
- partition: 哨兵(最后再将其归位) + 大循环 + 2 小循环, 交换元素法
- partition: 辅助数组 brr, 3 循环(3 次扫描 arr) 分别将小/等/大于 guard 的数加入 brr
- partition: 哨兵(最后再将其归位) + lo + hi, 外加 2 个动指针 leftLimit 与 rightLimit, 表示小于区的上界和大于区的上界
// lt eq gt three parts
void quick3waySort(int *a, int lo, int hi) {
if (hi <= lo) return;
int lt = lo, i = lo+1, gt = hi;
int v = a[lo];
while (i <= gt) {
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
Heap Sort
- Built on Priority Queue
- swap: 2NlgN + 2N (2NlgN for sink N times, 2N for construct MaxHeap)
- compare: NlgN + N (NlgN for sink N times, N for construct MaxHeap)
// MaxPQ
void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k/2, k);
k = k/2;
}
}
void sink(int k) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
Radix Sort
基数排序 (可用于混乱 shuffle 数组):
- 从个位到高位放入桶
- 从高位到个位放入桶
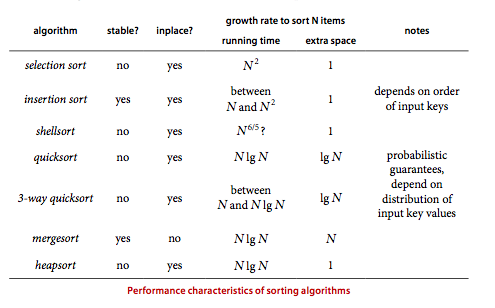
Tree Algorithm
Binary Search Tree
Hibbard Deletion
2-3 Tree
2-3 Tree is Balance Tree:
插入:
- 1+1=2node -> 3node
- 1+2=3node -> 4node -> 2node
- 将 4node 结点中间元素移至父结点, 其余 2 元素分离为子 2node 节点
Red-Black BST
- 基于 2-3Tree, 将 3node 用红色标记
- 关键: 将红色标记向上传递至根部
// is node x red; false if x is null ?
private boolean isRed(Node x) {
if (x == null) return false;
return x.color == RED;
}
// make a right-leaning link lean to the left
private Node rotateLeft(Node h) {
// assert (h != null) && isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = x.left.color;
x.left.color = RED;
x.size = h.size;
h.size = size(h.left) + size(h.right) + 1;
return x;
}
// make a left-leaning link lean to the right
private Node rotateRight(Node h) {
// assert (h != null) && isRed(h.left);
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = x.right.color;
x.right.color = RED;
x.size = h.size;
h.size = size(h.left) + size(h.right) + 1;
return x;
}
// flip the colors of a node and its two children
private void flipColors(Node h) {
// h must have opposite color of its two children
// assert (h != null) && (h.left != null) && (h.right != null);
// assert (!isRed(h) && isRed(h.left) && isRed(h.right))
// || (isRed(h) && !isRed(h.left) && !isRed(h.right));
h.color = !h.color;
h.left.color = !h.left.color;
h.right.color = !h.right.color;
}
// insert the key-value pair in the subtree rooted at h
private Node put(Node h, Key key, Value val) {
// insert/put new node as left/right child of leaf node
if (h == null) return new Node(key, val, RED, 1);
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if (cmp > 0) h.right = put(h.right, key, val);
else h.val = val;
// fix-up any right-leaning links
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
if (isRed(h.left) && isRed(h.right)) flipColors(h);
h.size = size(h.left) + size(h.right) + 1;
return h;
}
public void put(Key key, Value val) {
if (key == null) {
throw new IllegalArgumentException("first argument to put() is null");
}
if (val == null) {
delete(key);
return;
}
root = put(root, key, val);
root.color = BLACK;
// assert check();
}
// Assuming that h is red and both h.left and h.left.left
// are black, make h.left or one of its children red.
private Node moveRedLeft(Node h) {
// assert (h != null);
// assert isRed(h) && !isRed(h.left) && !isRed(h.left.left);
flipColors(h);
if (isRed(h.right.left)) {
h.right = rotateRight(h.right);
h = rotateLeft(h);
flipColors(h);
}
return h;
}
// Assuming that h is red and both h.right and h.right.left
// are black, make h.right or one of its children red.
private Node moveRedRight(Node h) {
// assert (h != null);
// assert isRed(h) && !isRed(h.right) && !isRed(h.right.left);
flipColors(h);
if (isRed(h.left.left)) {
h = rotateRight(h);
flipColors(h);
}
return h;
}
// restore red-black tree invariant
private Node balance(Node h) {
// assert (h != null);
if (isRed(h.right)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
if (isRed(h.left) && isRed(h.right)) flipColors(h);
h.size = size(h.left) + size(h.right) + 1;
return h;
}
// delete the key-value pair with the minimum key rooted at h
private Node deleteMin(Node h) {
if (h.left == null)
return null;
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = deleteMin(h.left);
return balance(h);
}
/**
* Removes the smallest key and associated value from the symbol table.
* @throws NoSuchElementException if the symbol table is empty
*/
public void deleteMin() {
if (isEmpty()) throw new NoSuchElementException("BST underflow");
// if both children of root are black, set root to red
if (!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = deleteMin(root);
if (!isEmpty()) root.color = BLACK;
// assert check();
}
// delete the key-value pair with the maximum key rooted at h
private Node deleteMax(Node h) {
if (isRed(h.left))
h = rotateRight(h);
if (h.right == null)
return null;
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
h.right = deleteMax(h.right);
return balance(h);
}
/**
* Removes the largest key and associated value from the symbol table.
* @throws NoSuchElementException if the symbol table is empty
*/
public void deleteMax() {
if (isEmpty()) throw new NoSuchElementException("BST underflow");
// if both children of root are black, set root to red
if (!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = deleteMax(root);
if (!isEmpty()) root.color = BLACK;
// assert check();
}
// delete the key-value pair with the given key rooted at h
private Node delete(Node h, Key key) {
// assert get(h, key) != null;
if (key.compareTo(h.key) < 0) {
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = delete(h.left, key);
}
else {
if (isRed(h.left))
h = rotateRight(h);
if (key.compareTo(h.key) == 0 && (h.right == null))
return null;
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
if (key.compareTo(h.key) == 0) {
Node x = min(h.right);
h.key = x.key;
h.val = x.val;
// h.val = get(h.right, min(h.right).key);
// h.key = min(h.right).key;
h.right = deleteMin(h.right);
}
else h.right = delete(h.right, key);
}
return balance(h);
}
/**
* Removes the specified key and its associated value from this symbol table
* (if the key is in this symbol table).
*
* @param key the key
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public void delete(Key key) {
if (key == null) throw new IllegalArgumentException("argument to
delete() is null");
if (!contains(key)) return;
// if both children of root are black, set root to red
if (!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = delete(root, key);
if (!isEmpty()) root.color = BLACK;
// assert check();
}
基本性质
- 非红即黑
- 根黑
- 叶黑 e.g T.null 黑哨兵
- 红父孩子黑
- 简单路径同黑
- 右孩子不红 e.g 父黑两孩红 -> 父红两孩黑(flip); 父黑右红 -> 父左旋变红, 右孩子变黑(left-rotate)
基本操作
- 插入(插入红点, 旋转+重新着色(反色)保持红黑性质)
- 删除(删除红点, 旋转+重新着色(反色)保持红黑性质)
B Tree
t: 每个内部结点至少 t 个孩子(t-1 个 key), 至多 2t 个孩子(2t-1 个 key)
插入/删除
下溯的同时,分裂满结点
Fibonacci Heap
BST + 循环双向链表:
- 一个根树(根结点)循环双向链表
- n 个孩子循环双向链表: 每个根树的每层结点形成一个循环双向链表
K-Dimensional Tree
- 分隔空间数据
e.g 左子树:左下方 右子树:右上方
Search Algorithms
First Search
- DFS(深度优先):栈实现
- BFS(广度优先):队列实现
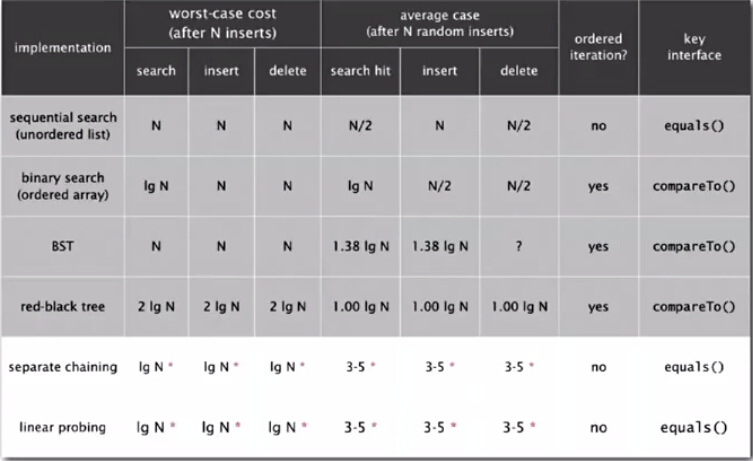
Cycle Detection
- 许多图论算法不适用于存在环路的复杂图,故使用循环检测剔除意外情况
处理方法:可将环路元素(如强联通分支)视作单一元素,忽视其内部结构
a = b+1;b = c+1;c = a+1;
//a extends b;b extends c;c extends a;
Dynamic Programming
- 最优解结构特征: 一个选择 + 子问题的最优解 - 所有(可重复求解)子问题的最优解可独立求解(不互相影响)
- 递归定义最优解: 列出递归表达式
- 自底向上求解最优解
- 构造最优解(额外信息数组)
子问题
- 子问题可映射为有向图, 并对其进行拓扑排序: 共有 O(n) 个子问题, 每个子问题最多 O(n) 种选择, 则算法时间复杂度为 O(n^2).其对应子问题图有 n 个顶点, 每个顶点最多有 n-1 条边.
- 递归生成可以重复求解的子问题,而不是不断生成新的子问题
范例
- 切割钢条问题:
max{p[i], r[n-i]} - 矩阵相乘链问题
- 最大公共子序列问题:
r[i, j]=max{r[i, j-1], r[i-1, j]} - 无权最短路径:
path[i, j]=min{path[i, r], [r, j]}
Greedy Algorithm
- 最优解结构特征: 一个选择 + 子问题的最优解 - 所有(可重复求解)子问题的最优解可独立求解(不互相影响)
- 递归定义最优解: 列出递归表达式
- 自底向上求解最优解: 每次不进行多次选择, 只进行一次 贪心选择
- 构造最优解(额外信息数组)
Map Algorithm
图的表示
- 邻接链表法
- 邻接矩阵法
稀疏矩阵
unordered_map< int, unordered_map<int, int> > // => (row, (col, val))
广度优先遍历
BFS Node Color
- white: 未被发现/访问
- gray: 已被发现(进入队列), 邻接结点未全部发现
- black: 已被发现, 邻接结点全部发现
BFS Node Parent
广度优先树父结点
BFS Node Distance
距离 = v.pi.d + 1
利用队列实现广度优先遍历
深度优先遍历
利用 递归/栈 实现深度优先遍历
DFS Node Color
- white: 未被发现/访问
- gray: 已被发现, 未二次访问
- black: 已被发现, 二次访问(比其深的所有结点皆被发现)
当第一个访问 edge(u,v) 时:
- v.color == white: 树边
- v.color == gray : 后向边(v 为 深度优先森林的祖父结点)
- v.color == black: 前向边/横向边(v 为较深的结点/子结点)
- 无向图深度优先遍历不会出现 前向边/横向边
DFS Node Parent
比 v 浅的结点(比 v 更早被发现的结点)
DFS Node Distance
- v.d = ++time: 被发现的时间戳(入栈)
- v.f = ++time: 被二次访问的时间戳(出栈)
- time
<v.d, white; v.d<time<v.f, gray: time>v.f, black
拓扑排序
目标集合: 拓扑排序后集合, 先入顶点高序, 后入顶点低序
Kahn 算法
不断将图中入度为 0 的点移入目标集合
DFS(深度优先)
当深度遍历至较深处, 并开始回溯时, 将此时访问的顶点加入目标集合(v.f 降序)
单源最短路径
void Relax(int u, int v, int w) {
if v.d > u.d + w[u][v] {
v.pi = u;
v.d = v.pi.d + w[v.pi][v];
}
}
DAG Shortest Paths
先将图进行拓扑排序(深度优先遍历), 再按照拓扑排序顺序, 依次对每个结点(拓扑排序)的邻接边进行 relax
a -> b -> c --> d, 且 a--b, a--c, b--d, c--d: relax(a, b), relax(a, c), relax(b, d), relax(c, d)
Bellman-Ford Algorithm
对每条边进行 n 次(结点总数) relax
Dijkstra Algorithm
贪心算法: 每次选取不属于 S 集合(white) 且 v.d 最小(gray)的结点, 对其所有邻接边进行 relax, 并将其加入 S 集合(black)
- white: 不属于 S 集合
- gray: 不属于 S 集合 且 v.d 最小
- black: 属于 S 集合
结点对最短路径
动态规划: l^m(i, j) = min(l^m-1(i, j), min(1 <= k <= n){l^m-1(i, k)+w(k, j)})
m: 中间结点个数
Floyd-Warshall Algorithm
d^k(i, j) = w(i, j), k = 0 | min(d^k-1(i, j), d^k-1(i, k) + d^k-1(k, j)), k >= 1
pi^(i, j) = pi^k-1(i, j) or pi^k-1(k, j)
k: 中间结点个数
Matrix floyd_warshall(Matrix W) {
int n = W.rows;
Matrix D^0 = W;
for (int k = 1;k < n+1; k++) {
D^k = new Matrix(n);
for (int i = 1; i < n+1; i++) {
for (int j = 1; j < n+1; J++) {
d^k[i][j] = min(d^k-1[i][j], d^k-1[i][k]+d^k-1[k][j]);
}
}
}
return D^n;
}
最大流问题
MaxFlow Problem:

最大流模型
最大流模型必须满足以下条件:
- 无双向边
- 唯一的源点 s 和 唯一的汇点 t
对于不符合该模型的问题可进行简单转化:
- 双向边: 添加额外结点, 切割双向边的其中一条, 使得双向边变成 3 条单向边
a --> b, b --> a: a --> c, c --> b, b --> a
- 多源点/汇点: 添加一个总源点/汇点
残存网络
- 若原图 u --> v 总容量 > 0, 则残存网络中 边 u --> v:剩余容量, 边 v --> u: 已用容量
- 增广路径: 残存网络中一条可行通路
最大流最小割定理
MaxFlow-MinCut Theorem:
- 切割的净流量: 流出-流入
- 切割的容量: 流出总容量(无需减流入总容量)
- 最小切割: 容量最小的切割
最大流最小割定理: 以下三个命题等价
- f 是 G 的一个最大流
- 残存网络 Gf 不含增广路径
- |f| = c(S, T)(切割的容量): |f|
<=c(S, T)(流网络中任意流 f<=任意切割容量 c(S, T))
Ford-Fulkerson Algorithm
不断寻找增广路径
Tree Edit Distance
Definition
Tree Edit Distance: 给定 Cost(edit operation) 时的最小编辑费用
Asymmetry of Verification and Verifiers Law
Asymmetry of verification and verifiers law:
所有可解决且易于验证的问题, 都将被 AI 解决.