Sorting

Summary

• 强制稳定: 增加(唯一)时间戳, 修改 CompareTo 接口定义 => 当主元素相同时, 时间戳小的元素更小

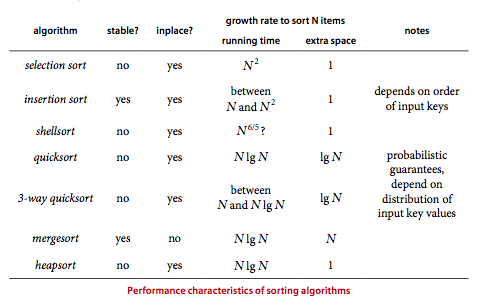
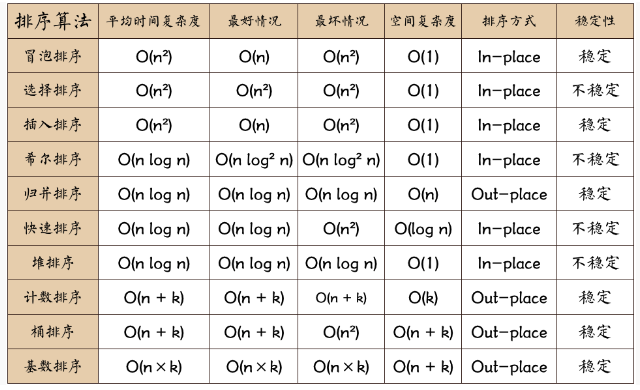
Selection Sort

• swap: O(n)
• compare: O(n^2)

Insertion Sort

• swap: O(n^2/4)
• compare: O(n^2/4)

Shell Sort

• swap: O(n^2/4)
• compare: O(n^2/4)

Merge Sort

• 利用 Merge Sort 计算逆序对个数: left[i] > right[j] => inversions += (mid - i + 1), 即所有 i~mid 元素都与 j 元素为逆序对

    // merge and count
    private static long merge(int[] a, int[] aux, int lo, int mid, int hi) {
        long inversions = 0;

        // copy to aux[]
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k];
        }

        // merge back to a[]
        int i = lo, j = mid+1;
        for (int k = lo; k <= hi; k++) {
            if      (i > mid)           a[k] = aux[j++];
            else if (j > hi)            a[k] = aux[i++];
            else if (aux[j] < aux[i]) { a[k] = aux[j++]; inversions += (mid -
            i + 1); }
            else                        a[k] = aux[i++];
        }
        return inversions;
    }

    // return the number of inversions in the subArray b[lo..hi]
    // side effect b[lo..hi] is rearranged in ascending order
    private static long count(int[] a, int[] b, int[] aux, int lo, int hi) {
        long inversions = 0;
        if (hi <= lo) return 0;
        int mid = lo + (hi - lo) / 2;
        inversions += count(a, b, aux, lo, mid);
        inversions += count(a, b, aux, mid+1, hi);
        inversions += merge(b, aux, lo, mid, hi);
        assert inversions == brute(a, lo, hi);
        return inversions;
    }

    /**
     * Returns the number of inversions in the integer array.
     * The argument array is not modified.
     * @param  a the array
     * @return the number of inversions in the array. An inversion is a pair of
     *         indices {@code i} and {@code j} such that {@code i < j}
     *         and {@code a[i]} > {@code a[j]}.
     */
    public static long count(int[] a) {
        int[] b   = new int[a.length];
        int[] aux = new int[a.length];
        for (int i = 0; i < a.length; i++)
            b[i] = a[i];
        long inversions = count(a, b, aux, 0, a.length - 1);
        return inversions;
    }

    // return Kendall tau distance between two permutations
    public static long distance(int[] a, int[] b) {
        if (a.length != b.length) {
            throw new IllegalArgumentException("Array dimensions disagree");
        }
        int n = a.length;

        int[] ainV = new int[n];
        for (int i = 0; i < n; i++)
            ainV[a[i]] = i;

        Integer[] bNew = new Integer[n];
        for (int i = 0; i < n; i++)
            bNew[i] = ainV[b[i]];

        return Inversions.count(bNew);
    }

Quick Sort

• partition: 哨兵(最后再将其归位) + 大循环 + 2 小循环, 交换元素法
• partition: 辅助数组 brr, 3 循环(3 次扫描 arr) 分别将小/等/大于 guard 的数加入 brr
• partition: 哨兵(最后再将其归位) + lo + hi, 外加 2 个动指针 leftLimit 与 rightLimit, 表示小于区的上界和大于区的上界

// lt eq gt three parts
void quick3waySort(int *a, int lo, int hi) {
    if (hi <= lo) return;
    int lt = lo, i = lo+1, gt = hi;
    int v = a[lo];

    while (i <= gt) {
        int cmp = a[i].compareTo(v);
        if      (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else i++;
    }

    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

Heap Sort

• Built on Priority Queue
• swap: 2NlgN + 2N (2NlgN for sink N times, 2N for construct MaxHeap)
• compare: NlgN + N (NlgN for sink N times, N for construct MaxHeap)

// MaxPQ
void swim(int k) {
    while (k > 1 && less(k/2, k)) {
        exch(k/2, k);
        k = k/2;
    }
}

void sink(int k) {
    while (2*k <= N) {
        int j = 2*k;
        if (j < N && less(j, j+1)) j++;
        if (!less(k, j)) break;
        exch(k, j);
        k = j;
    }
}

Radix Sort

基数排序 (可用于混乱 shuffle 数组):

• 从个位到高位放入桶
• 从高位到个位放入桶